Stiffness

Modulus of Elasticity, E

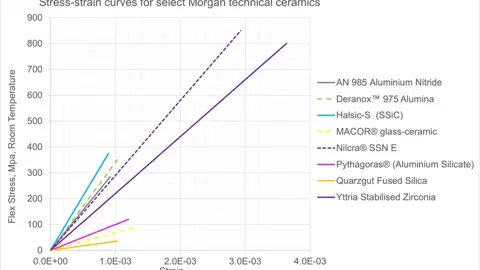
Elastic Modulus, also referred to a Modulus of Elasticity or Young’s Modulus, is a measure of a material’s stiffness and is the ratio of the amount of stress applied to a material divided by the amount of elastic (reversible) strain that the applied stress induces. For ceramics, the value is most often obtained from a static bending test, by calculating the slope of the resulting stress-strain curve.

Higher porosity levels within a ceramic will reduce the material’s Elastic modulus.

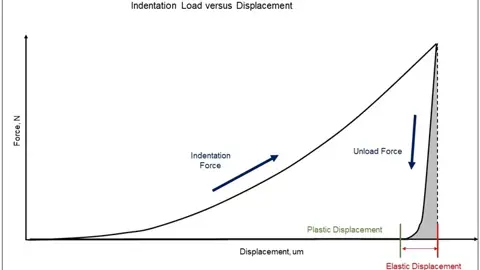
Indentation Modulus

Indentation modulus, EIT, can be a close approximation of the Elastic modulus. It is obtained by using a nanoindentation technique. Unlike a hardness test where a constant load is applied, to obtain EIT the load is gradually increased and then decreased. During the test, load versus displacement is plotted and reveals the amount of plastic and elastic displacement that occurred. The indentation modulus is calculated using the elastic displacement portion of the curve (the portion derived when the load is decreased).

Non-destructive sound waves can also be used to indirectly measure a material’s Elastic Modulus [in addition to Poisson’s ratio, Shear modulus (G), and Bulk Modulus (K)], but only if the material is homogeneous, isotropic, and nondispersive (meaning the velocity of the sound transmission through the material does not change with the frequency of the sound wave). This method is referred to as an ultrasonic pulse-echo technique or ultrasound point analysis (UPA). For best results, test samples should have parallel surfaces and minimal surface roughness. During the method, an ultrasonic transducer transmits and received acoustic signal through the sample and measures the elapsed time it takes for the signal to travel though the sample and return. Dividing 2x the sample thickness by this elapsed time provides the velocity of the sound. This velocity is determined for both the longitudinal and transverse (shear) directions of the test sample. Poisson’s ratio can then be calculated contrasting the two velocity values. Using the measured density of the sample, the calculated Poisson’s ratio, and the measured longitudinal velocity, the Elastic modulus (or Sonic Modulus) can be calculated.

Other non-destructive methods rely upon inputs to establish a vibration within the sample. These dynamic or resonant frequency methods either rely upon acoustic waves (Resonant Ultrasound Spectroscopy, RUS) or upon a singular elastic strike with an impulse tool (Impulse excitation, IE) to establish a mechanical vibration of the sample. Given the known values of the sample’s mass, geometries, and either initial estimates of Modulus (Elastic, Bulk, or Shear) and Poisson’s ratio for the RUS method, or a determination of the resonance frequencies of the sample for the IE method, the dynamic Elastic Modulus, dynamic shear modulus, and Poisson’s ratio can be calculated.

Because elastic modulus and hardness are both measures of a material’s resistance to deformation (strain) under load (stress), elastic modulus and hardness values tend to correlate to each other. Accordingly, because silicon carbide and silicon nitride are very hard ceramics, the also have high Elastic Modulus.

High hardness values, like high elastic modulus values, are characteristic of rigid materials that will fail in a brittle manner versus a ductile manner.

Shear Modulus, G

Shear modulus, also referred to as the Modulus of Rigidity, is the ratio of shear stress applied to a sample divided by the resulting amount of shear strain. For example, if a cube is subjected to a force parallel to one of its faces and subjected to an equal opposite force parallel to the opposite face, its sideview will deform from a square into trapezoid. The modulus is the amount of shear stress applied (before plastic deformation occurs) divided by the amount elastic deformation (strain).

For ceramics the shear modulus is typically about 40% of the elastic modulus.

For isotropic materials, the following equation defines the relationship between Elastic modulus (E), Shear Modulus (G), Bulk Modulus (K), and Poisson’s ratio (μ): E = 2G (1 + μ) = 3K (1 -2μ)

*Typical values at room temperature

Bulk Modulus, K

Bulk Modulus is the ratio of the amount of isostatic pressure (equal pressure applied to a sample from all directions) divided by the resulting amount of elastic volumetric strain of the sample. For ceramics, the bulk modulus is typically equal to or slightly higher than the shear modulus.