Bending Strength

Bending strength, or flexural strength, of ceramics is usually obtained by performing either 3-point or 4-point bending tests on test bars of either rectangular or circular cross sections. Besides being influenced by the ceramic material’s grain size, porosity, and internal flaws, test results can be negatively impacted by machining technique if the technique introduces flaws or cracks on or near the surface or on the edges of the test bar. Because the highest tensile stress will occur on a surface of the test bar, surface flaws will dominate as the cause of fracture of the test coupon. Accordingly, the 4-point bending test is often preferred over the 3-point test because the 4-point test coupon is more susceptible to internal flaws due to the more uniform stress applied to a larger volume of the coupon. Likewise, for the same geometry of test coupon, strengths resulting from 3-point bending tests are typically higher than strength results from 4-point tests. Therefore, it is important to note the test method when reporting results.

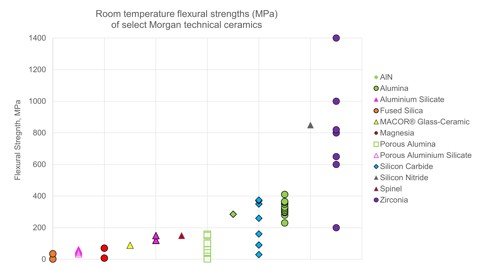
Technical ceramics are very stiff or rigid, meaning they resist bending. Many technical ceramics resist bending (maintaining their bending strengths) up to their maximum use temperature.

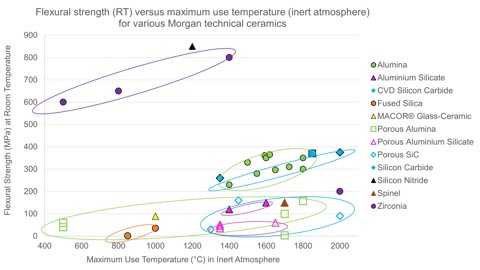
Note: At elevated temperatures, flexural strengths can be lower than room temperature values

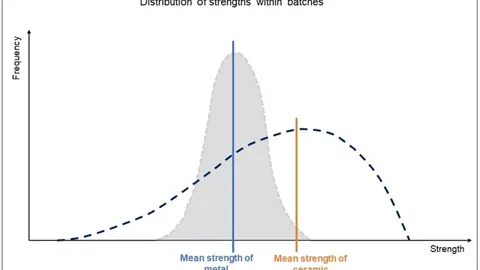
The strengths of ceramics are influenced by their grain size, porosity, and degree of homogeneity, and because these characteristics can vary batch-to-batch depending upon the effectiveness of process controls and other factors, the statistical distribution of strength properties of ceramics can be a wider distribution than those of metallic alloys. Consequently, when reporting the strength of a ceramic, it is useful to describe the shape of the distribution of set of measured strength values.

Weibull Modulus, m

In 1937, the mathematician, engineer, and scientist Waloddi Weibull described a distribution of likely strength results which became known as the Weibull distribution. The distribution assumes the failure of the set of test coupons is caused by single failure source (e.g. the presence of a structural inhomogeneity). The Weibull modulus of this distribution is a parameter that quantifies the effective width of the distribution curve when using a strength value, σo, that represents the stress at which the probability of failure is 63.2%. A material with a high Weibull modulus value has a narrower distribution of stress values versus a material with a low Weibull modulus.

Reported Weibull modulus values for technical ceramics for bending strengths, using a 4-point bending test method at room temperature, generally range between 10 and 30.